Lab 6 - Modelowanie i symulacja systemów robotycznych w ROS’ie
Modelowanie i sterowanie robotów - laboratorium
Lab 6 - Modelowanie i symulacja systemów robotycznych w ROS’ie
Politechnika Poznańska
Instytut Robotyki i Inteligencji Maszynowej

Jakub Chudziński, Bartłomiej Kulecki
Uruchomienie ROS'a
Uruchom system zgodnie z instrukcją do zajęć nr 4.
O modelowaniu i symulacji systemów robotycznych
Narzędzia do programowania robotów przemysłowych i symulacji ich pracy pozwalają na tworzenie modeli procesów wytwórczych. Sprawdzają się świetnie, jeśli chodzi o wstępne przygotowanie programu dla robota, pozwalając na redukcję czasu cyklu pracy robota i skracając przy tym czas pracy robotyka na rzeczywistym sprzęcie. Język programowania w przypadku tego typu narzędzi jest zależny od robota.
Główną zaletą ROS'a jest jednak zupełnie coś innego - zdolność do integracji modułów dla wielu podsystemów, pozwalająca na tworzenie zaawansowanych robotycznych aplikacji (ang. robotics middleware). Pomimo to, istnieją w ROS'ie środowiska do symulacji (Gazebo, RViz) dedykowane złożonym systemom i użytkownikom, którzy posiadają umiejętności programowania w C++ lub Pythonie, niezależnie od wykorzystywanych robotów, czy sensorów.
W przypadku Process Simulate istnieje nawet możliwość integracji z ROS'em, co wskazuje na różne przeznaczenie obu aplikacji. W praktycznym zastosowaniu, zamodelowanie całego otoczenia pracy robota, przykładowo warsztatu w jakim docelowo się znajdzie, jest prostsze do "przeklikania". Natomiast ROS mógłby odpowiadać za bezkolizyjne sterowanie robotem, który samodzielnie lokalizuje obiekty do chwytania za pomocą systemu wizyjnego (kamer i algorytmów). W czasie realizacji zadania może być konieczne wysterowanie chwytaka, a także może się zdarzyć przejazd w pobliżu konfiguracji osobliwych robota, warto to przewidzieć na etapie modelowania.
Modelowanie i symulacja narzędzia pracy
PG70 to chwytak znajdujący zastosowanie w aplikacjach pick-and-place niewielkich detali. Szczegóły techniczne dostępne są online.
| Chwytak PG+70 | Model PG+70 |
|---|---|
 |
 |
Rzeczywiste narzędzia mogą być sterowane przykładowo elektrycznie, czy pneumatycznie. Robotyk po podłączeniu chwytaka, zmieniając odpowiedni bit w rejestrach, otwiera lub zamyka zaciski. ROS częściowo abstrahuje użytkownika od niskopoziomowego programowania udostępniając gotowe moduły do sterowania.
Załaduj samodzielnie przedstawiony chwytak
Uruchom terminal, przejdź do katalogu ze środowiskiem ROSa (np.catkin_ws), ustaw źródła (source devel/setup.bash) oraz uruchom plik launch o nazwiemy_application.launchz parametremgripper:=pg70z paczkipilz_tutorial.
Układy współrzędnych związane z chwytakiem
Dodaj w RVizie moduł TF i w oknie symulacji przejrzyj układy współrzędnych, które są związane z chwytakiem. Rozwijając menu z nazwą układu współrzędnych odczytaj układ nadrzędny (bazowy) oznaczony jakoParent.
- Do czego przyłączony jest chwytak (
prbt_gripper_palm_link)?- Wyświetl układ TCP (
prbt_tcp). Czy jest różnica w jego umiejscowieniu przed i po załadowaniu chwytaka? Możesz spróbować zresetować symulację i załadować robota bez chwytaka dla porównania.- Wyżej wymieniony "gotowy moduł do sterowania" chwytaka jest dostępny open-source, tak jak większość oprogramowania w ROS'ie. Posiada on definicję struktury kinematycznej (w formacie URDF) i gotowe komendy sterujące. Za integrację z robotem PRBT odpowiedzialny jest moduł prbt_grippers, dzięki temu TCP dostosowuje się automatycznie po załadowaniu chwytaka.
Wysterowanie chwytaka
Korzystając z API w Pythonie zmień położenie zacisków chwytaka.
- Wprowadź zmiany w swoim pliku
ImieApplication.py.- Przykładowy kod, może wyglądać następująco:
#!/usr/bin/env python3
from geometry_msgs.msg import Pose, Point
from pilz_robot_programming import *
import math
import rospy
__REQUIRED_API_VERSION__ = "1" # API version
__ROBOT_VELOCITY__ = 0.5 # velocity of the robot
# main program
def start_program(r: Robot):
r.move(Gripper(goal=0.02, vel_scale=0.02))
if __name__ == "__main__":
# init a rosnode
rospy.init_node('robot_program_node')
# initialization
r = Robot(__REQUIRED_API_VERSION__) # instance of the robot
# start the main program
start_program(r)Manipulacja obiektami a aspekt osobliwości
Źródło osobliwości
Przekształcenie liniowe wiążące prędkości w poszczególnych węzłach z prędkościami kartezjańskimi końcówki nazywane jest jakobianem prędkości. Poszukując źródła osobliwości, stawiamy pytanie - czy ta macierz jest odwracalna? To znaczy, czy nie jest osobliwa? Jeśli macierz nie jest osobliwa, to możemy ją odwrócić, aby obliczyć prędkości w poszczególnych węzłach dla danych prędkości kartezjańskich. Jest to istotne, jeśli zależy nam, aby chwytak poruszał się z zadaną prędkością w przestrzeni kartezjańskiej. Konfiguracje, przy których jakobian staje się osobliwy, nazywane są osobliwościami manipulatora.
Porównanie osobliwości ramienia robota i człowieka
Powołując się kolejny raz na porównanie ludzkiej ręki do ramienia robota, możesz spróbować odtworzyć osobliwość. Możliwe, że po takim ćwiczeniu łatwiej Ci będzie zapamiętać konfiguracje osobliwe manipulatorów i staną się one bardziej intuicyjne. Przedstawimy jedną z trzech występujących w robotach 6 osiowych, kiedy to oś 4 (obrót przedramienia) i 6 (obrót opuszkami palców) położone są w jednej linii. Zauważycie utratę stopnia swobody (tzn. obrót palcami i przedramieniem się nakładają). Jest to najczęstsza osobliwość (zwana osobliwością nadgarstka - w manipulatorach 3 ostatnie osie tworzą nadgarstek).
Aby dobrze zrozumieć przyczynę osobliwości, warto odnieść się do ludzkich osobliwości, wykorzystywanych również w robotach humanoidalnych. Roboty przemysłowe są programowane tak, aby unikać osobliwych konfiguracji ze względu na opisany wcześniej problem ze sterowaniem końcówką. W przypadku człowieka, osobliwości są wykorzystywane bardzo często, ponieważ w tych konfiguracjach osiąga się maksymalną sztywność ramion (zmniejszając użycie siły), sterowanie jest zdecydowanie bardziej zaawansowane. Problemem nie jest więc sama struktura kinematyczna, lecz metoda sterowania oparta o odwracanie jakobianu.
\[ \bar{\dot{q}} = {J^{-1} \cdot \bar{v}} \]
W powyższym wzorze \(\bar{v}\) to wektor składający się z 6 elementów reprezentuących prędkości liniowe i kątowe, a \(\bar{\dot{q}}\) to wektor prędkości poszczególnych węzłów. Celem stosowania jakobianu jest obliczenia docelowych prędkości węzłowych dla danych prędkości w przestrzeni kartezjańskiej.
Cechy konfiguracji osobliwych
Wszystkie manipulatory mają osobliwości przy granicy ich przestrzeni roboczej, a większość ma miejsca osobliwe wewnątrz ich przestrzeni roboczej. W pobliżu konfiguracji osobliwych prędkości w węzłach gwałtownie rosną do momentu przekroczenia maksymalnych wartości, następnie robot się zatrzymuje. Konfiguracjom osobliwym towarzyszy utrata stopnia swobody.
Przykład osobliwości nadgarstka
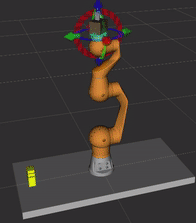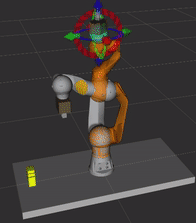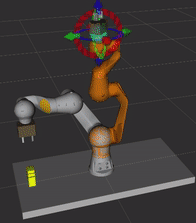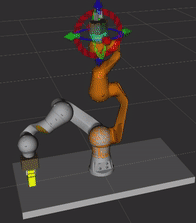
Osobliwość nadgarstka jest cechą wszystkich robotów 6 osiowych, niezależnie od struktury nadgarstka. Występuje, gdy osie przegubów 4 i 6 są ułożone równolegle - dzieje się tak, gdy kąt osi 5 jest równy 0. Robot przedstawiony na poniższym obrazku przecina konfigurację osobliwą. Gdyby zadać ruch we współrzędnych kartezjańskich w linii prostej przechodzący przez konfigurację osobliwą, osie 4 i 6 obracałyby się nie powodując przy tym ruchu końcówki i robot by się zatrzymał. W symulacji nie będzie możliwe zaplanowanie takiego ruchu ze względu na przekroczenie limitów prędkości.
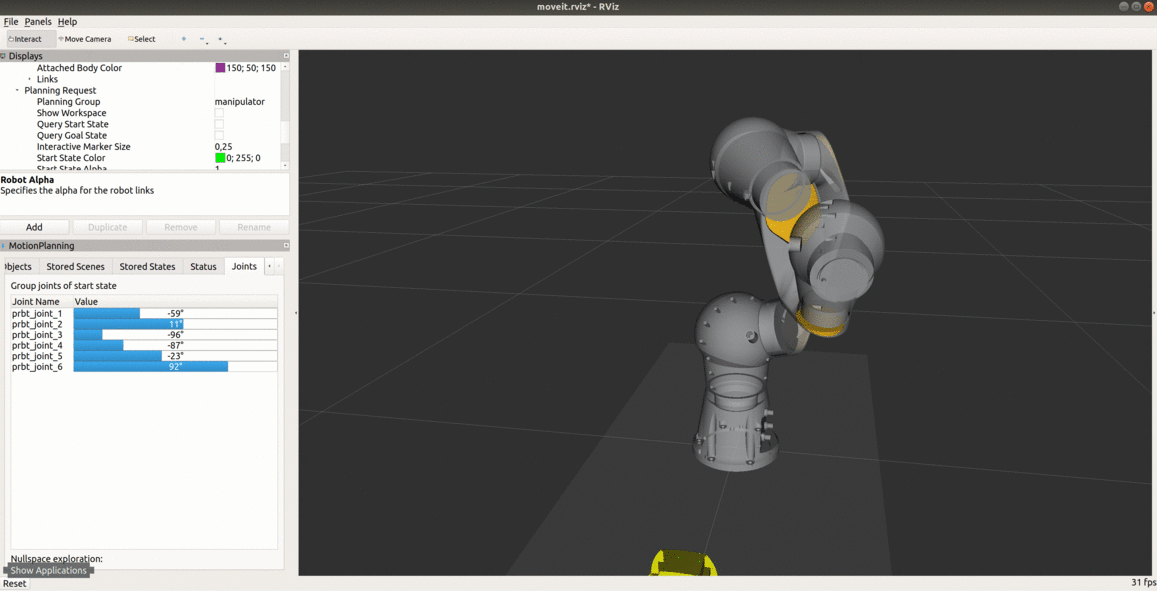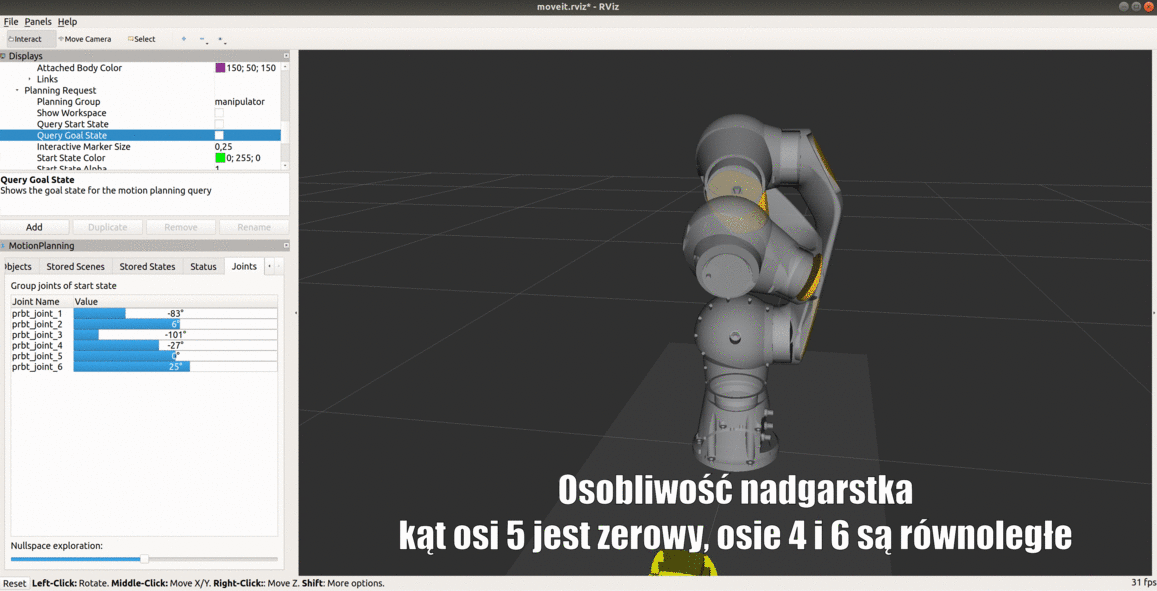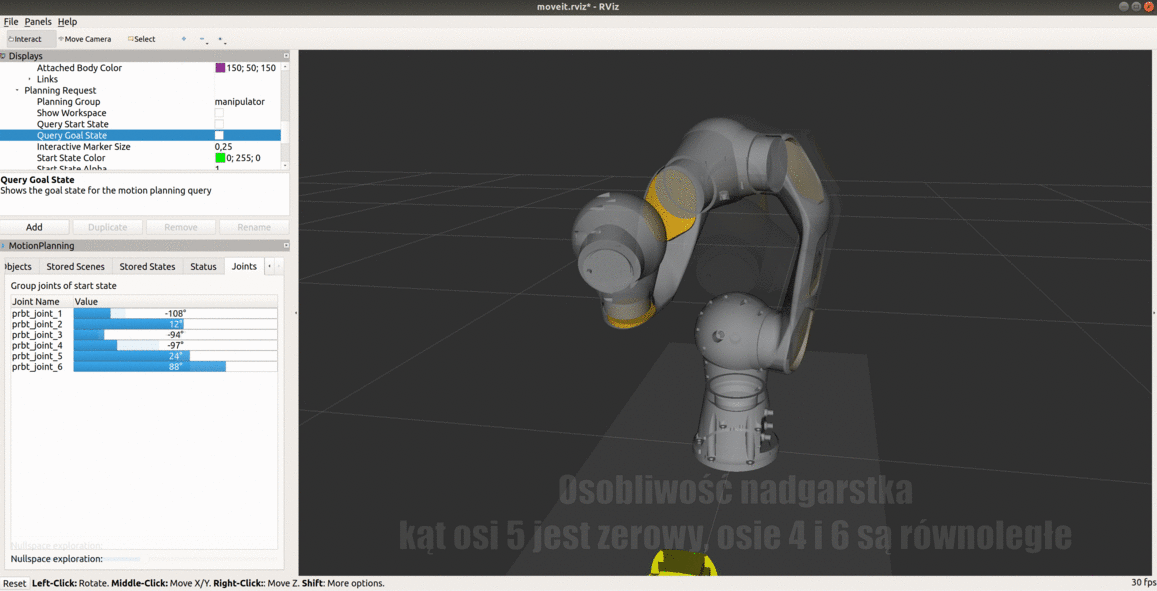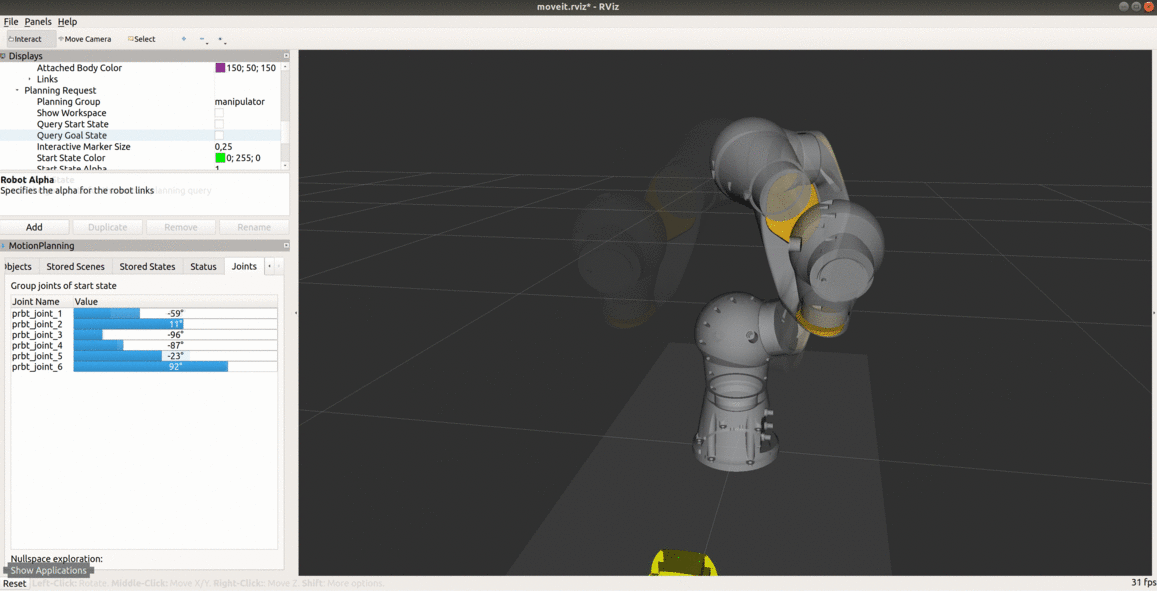
Zapoznaj się z osobliwością nadgarstka
Uruchom terminal, przejdź do katalogu ze środowiskiem ROSa (np.catkin_ws), ustaw źródła (source devel/setup.bash) oraz uruchom plik launch o nazwiemy_application.launchz paczkipilz_tutorialbez nadgarstka (pomińgripper:=pg70). Ustaw planowanie ruchu w tryb PTP i przejdź do zakładki Joints. Ustaw robota w konfiguracji podobnej do tej z powyższego obrazka, gdy końcowka jest zwrócona w prawą stronę (q̅=[-59, 11, -96, -87, -23, 92]). Wciśnij Plan & Execute, aby wykonać trajektorię. Przesuń robota w linii prostej w kierunku ujemnej osi y TCP. Zauważ, że już przy przesuwaniu końcówki, że osie 4 i 6 obracają się w nietypowy sposób (niewielkie przesunięcie końcówki powoduje duże zmiany kątowe w węzłach). Zwróć uwagę, że wypustka na flanszy pozostaje w tym samym miejscu. Zanim wykonasz zaplanowany ruch, spróbuj zmienić tryb ruchu na liniowy w oknie Context. Jaki błąd odczytasz w terminalu? Zaplanuj ruch w trybie PTP, przy wykonaniu zwróć uwagę na kształt trajektorii - czy jest to linia prosta?
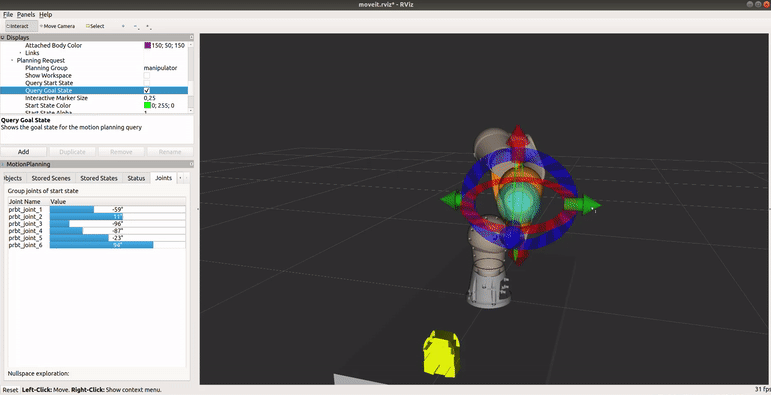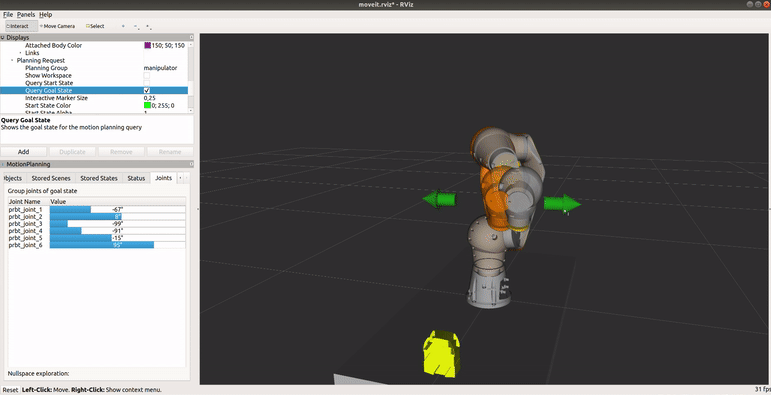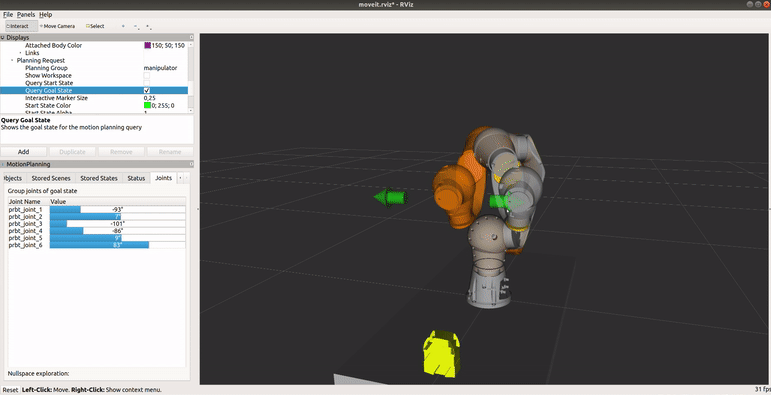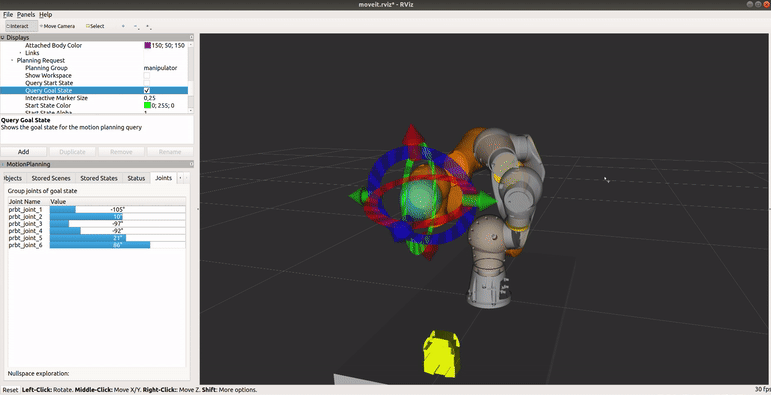
Sposoby unikania otoczenia konfiguracji osobliwych
W dalszej części skupimy się na omijaniu konfiguracji osobliwych w robotach 6 osiowych. Roboty reduntantne (DOF>6) mają zwiększoną rożnorodność sposobów osiągania póz, przez co osobliwości nie mają znaczącej wagi.
Dwie metody omijania konfiguracji bliskich osobliwym:
- Dodanie punktu pośredniego. Istotne jest, aby dobrany punkt oddalał nas od konfiguracji osobliwej. Kształt ścieżki ulega modyfikacji.
- Modyfikacja orientacji, utrzymując ten sam kształt ścieżki.
Zachowanie w przypadku zatrzymania robota z powodu przekroczenia prędkości w pobliżu konfiguracji osobliwej
W przypadku, gdy podczas zaplanowanej trajektorii (np. z wykorzystaniem teach-pendantu) robot gwałtownie przyspieszy i się zatrzyma, najbezpieczniejszym wyjściem z sytuacji jest ręczne oddalenie robota od tej konfiguracji ruchem w poszczególnych węzłach. Dany punkt trajektorii należy zmodyfikować.
Pamiętajmy, że osobliwości to temat będący zarzewiem dyskusji dla każdego robotyka, a sposoby ich unikania są pożądaną wiedzą i umiejętnością.
💥 🔥 Zadania do wykonania: 💥 🔥
W oparciu o dokumentację zaimplementuj poniższe zadania, w niektórych przypadkach dobierz odpowiedni rodzaj ruchu oraz układ odniesienia. Posłuż się swoim plikiem ImieApplication.py (po wprowadzeniu zmian wywołuj go komendą rosrun pilz_tutorial ImieApplication.py).
*Zadaj współczynnik skalujący prędkości dla ruchów PTP i LIN równy 0.4, dla otwierania chwytaka 0.1.
**Pozycja określona jest jako składowe x, y, z, a dla chwytaka jako szerokość rozwarcia.
***Orientacja określona jest w postaci obrotów Eulera wykonywanych w kolejności ZYZ wokół nowych osi (ang. intrinsic). Podane kąty wyrażone są w stopniach.
Zadanie 1
Uchwyć obiekt. Ustaw robota w konfiguracji z chwytakiem nakierowanym na obszar manipulacji, następnie wykonaj ruch dojazdowy nad żółty obiekt, otwórz chwytak, dojedź do obiektu utrzymując taką samą orientację i zamknij chwytak. Posłuż się poniższą tabelą, samodzielnie uzupełnij miejsca z 🔧.
| Nr | Rodzaj ruchu* | Układ odniesienia | Pozycja** | Orientacja*** |
|---|---|---|---|---|
| 1 | Ptp | prbt_base_link | (0,-0.25, 0.5) | (0, 180, 90) |
| 2 | Ptp | pnoz | (0, 0, 0.25) | (0, 180, 0) |
| 3 | Otwórz chwytak | Gripper | 0.03 | - |
| 4 | 🔧 | 🔧 | (0, 0, 0) | (0, 180, 0) |
| 5 | Zamknij chwytak | Gripper | 0.017 | - |
Zadanie 2
Podnieś chwytak o 0.25 m (6), przesuń o 0.1 m w kierunku osi y i obróć wokół osi -x o 60 stopni (7), a następnie przesuń w poziomie o 0.3 m w kierunku ujemnego y (8,9). Wykonaj ruch pośredni, który oddali końcówkę robota od konfiguracji osobliwej (8). Dodanie ruchu pośredniego spowoduje odkształcenie ścieżki i ominięcie konfiguracji osobliwej. Zaobserwuj efekt i nazwij rodzaj osobliwości. Możesz poeksperymentować dobierając inne położenie punktu pośredniego (dodając przesunięcie w innej osi) lub dodać więcej punktów pośrednich. Posłuż się poniższą tabelą, samodzielnie uzupełnij miejsca z 🔧.
| Nr | Rodzaj ruchu* | Układ odniesienia | Pozycja** | Orientacja*** |
|---|---|---|---|---|
| 6 | 🔧 | prbt_tcp | (0, 0, -0.25) | (0, 0, 0) |
| 7 | Ptp | prbt_tcp | (0, 0.1, 0) | (90, -60, 0) |
| 8 | 🔧 | prbt_tcp | (0, -0.1, 0) | (0, 0, 0) |
| 9 | Lin | prbt_tcp | (0, -0.2, 0) | (0, 0, 0) |

Zadanie 3
W poprzednich zadaniach planer ruchu w każdym punkcie planował kolejny ruch. Zastosuj obiekt typu Sequence(), dodaj do trajektorii poniższe ruchy, tak aby robot nie zatrzymywał się w trakcie ich realizacji. Ustaw parametr blend_radius=0.01 w przypadku pierwszego z poniższych ruchów.
| Nr | Rodzaj ruchu* | Układ odniesienia | Pozycja** | Orientacja*** |
|---|---|---|---|---|
| 10 | Lin | prbt_tcp | (0, 0, -0.1) | (0, 0, 0) |
| 11 | Lin | prbt_tcp | (-0.1, 0, -0.1) | (0, 0, 0) |
Zadanie 4 (dla chętnych)
Napisz program realizujący trajektorię podobną do tej z zadania 3. z zajęć nr 3 (rysowanie okręgu robotem Panda):
- Niech robot rozpocznie ruch od pozycji oznaczonej numerem 1 w tabeli z zadania 1. Następnie niech ustawi się nad żółtym obiektem, zjedzie w dół i wykona pełny okrąg wokół niego. Później niech ramię się podniesie i wróci do pozycji początkowej.
- Wykorzystaj w odpowiednich miejscach ruchy PTP, LIN, CIRC.
- Skorzystaj z obiektu typu
Sequence()i ustaw parametryblend_radius, tak aby trajektoria wykonywała się płynnie.
Zadanie domowe
Jeśli nie udało Ci się wykonać wszystkich zadań podczas laboratorium, dokończ je w domu.