Fourier transform

Introduction

In mathematics, the Fourier transform (FT) is a transform that converts a function into a form that describes the frequencies present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made the Fourier transform is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into terms of the intensity of its constituent pitches. ^[source]

Discrete-time Fourier transform of an infinite signal

$$ X\left(e^{j \omega}\right)=\sum_{n=-\infty}^{\infty} x\left(n T_{s}\right) e^{-j \omega n} $$ $$ x\left(n T_{s}\right)=\frac{1}{2 \pi} \int_{-\pi}^{\pi} X\left(e^{j \omega}\right) e^{j \omega n} d \omega $$

Discrete-time Fourier transform of a non-infinite signal :

$$ X(k)=\sum_{n=0}^{N-1} x(n) e^{-j \frac{2 \pi}{N} k n}, k=0,1,2 \ldots N-1$$ $$ x(n)=\frac{1}{N} \sum_{k=0}^{N-1} X(k) e^{j \frac{2 \pi}{N} k n}, n=0,1,2 \ldots N-1 $$ Implementation can look like this:

import numpy as np
def dft(x):
    x = np.asarray(x, dtype=float)
    N = x.shape[0]
    n = np.arange(N)
    k = n.reshape((N, 1))
    M = np.exp(-2j * np.pi * k * n / N)
    return np.dot(M, x)

Fast Fourier transform (fft)

The computational complexity of implementing discrete Fourier transform is O(N^2). A more efficient method is to use the fast Fourier transform algorithm (O(Nlog(N))), based on the radix-2 algorithm.

Analyze the difference in transformation execution time between the dft function and the built-in fft function:

x = np.random.random(1024)
np.allclose(dft(x), np.fft.fft(x)) #check if the results of both methods are similar

%timeit dft(x)
%timeit np.fft.fft(x)

Nyquist Frequency and Shannon's Theorem Nyquist frequency is the maximum frequency of spectral components of a signal subjected to the sampling process that can be reconstructed from a sequence of samples without distortion. Spectral components with frequencies higher than the Nyquist frequency become superimposed on components with other frequencies during sampling (aliasing phenomenon), which causes them to no longer be correctly reconstructed.

According to the sampling theorem, for uniform sampling with a sampling interval (T_{s}), the condition for signal reconstruction is that the maximum signal frequency does not exceed half of the sampling frequency, (f_{max}<f_{s}/2) or (f_{max}<1/{2T_{s}}).

Let's assume that there is a code generating a harmonic signal:

import pylab as py
import numpy as np
from numpy.fft import rfft, rfftfreq

def sin(f = 1, T = 1, fs = 128, phi =0 ):
    dt = 1.0/fs
    t = np.arange(0,T,dt)
    s = np.sin(2*np.pi*f*t + phi)
    return (s,t)    

Try to generate and display the Fourier transform in the form of the magnitude (the transform is complex) and 2 plots containing the real and imaginary parts. Based on the formula for the DFT, provide the frequency in Hz instead of samples.

from scipy.fft import fft, fftfreq
fs = 100
T = 1

(y,t) = sin(f = 10.0, T=T, fs=fs)

N=int(fs*T)

yf = fft(y)
xf = # fill
import matplotlib.pyplot as plt
plt.stem(xf, np.abs(yf), use_line_collection=True)
plt.grid()
plt.show()

In the next part, instead of manually calculating the frequency vector, you can use the fftfreq function:

xf = fftfreq(N, 1/fs)

However, you need to know how this vector is generated and what is the value of a single frequency quantum (the spectral resolution).

Tasks

1. Please generate a signal \(s(t)=sin(2\pi\cdot t \cdot 1)+sin(2\pi \cdot t\cdot3+\pi/5)\) of lengths 1, 2.5s and 3s, sampled at 100 Hz, calculate its Fourier transform using fft (\(X=fft(s)\)). How do the observed spectra differ and what could be the reasons for these differences?

2. The Fourier transform is reversible. Try to reconstruct the time waveform using ifft (\(\hat{x} = ifft(X)\)). Plot the original and reconstructed signals on the same graph. Note: the ifft function returns a vector of complex numbers. Check what its imaginary part is. In the reconstruction plot, show its real part. What is the accuracy of the reconstruction if the signal has a length of 3s? Define the accuracy of reconstruction as the root mean square error (RMSE): $$ RMSE=\sum_{i=0}^N \frac{1}{N}\cdot \sqrt{(s(i)- Re(\hat{x} i))^2} $$

3. Load data form a file containing EMG signals using pandas. The signal sampling frequency is 5120Hz, and the file contains recordings from 24 channels of EMG from the forearm muscles during various hand gestures. In further analysis, use the EMG_15 channel.

   • Identify the frequencies of the 3 strongest components with an impulse spectrum.
   • Try to perform 10-time downsampling (selecting every 10th sample of the signal), plot the original and downsampled spectra on one figure, and try to explain the observed differences.

EMG

Electromyography (EMG) is a technique for evaluating and recording the electrical activity produced by skeletal muscles. EMG is performed using an instrument called an electromyograph to produce a record called an electromyogram. An electromyograph detects the electric potential generated by muscle cells when these cells are electrically or neurologically activated. ^[source]

^ Gathering of the EMG dataset. ^[source]

EMG signal can be processed many different ways. In the field of classification (for example gesture recognition) it usually contains:

1. Preprocessing - signal filtration, removal of motion artifacts, network interference, training
2. Signal normalization
3. EMG signal detection (activity detection)
4. Feature extraction in a sliding window. Features are computed in a window of length 100ms - 1s, and the window is shifted by a "stride" that determines the frequency of the classifier's operation. In the case of multi-channel EMG, features are usually computed separately for each channel.
5. Classification/regression - in the basic version, it is implemented by a non-recursive system.

Feature extraction

In the current exercise, we rely on several basic amplitude features determined in a moving window:

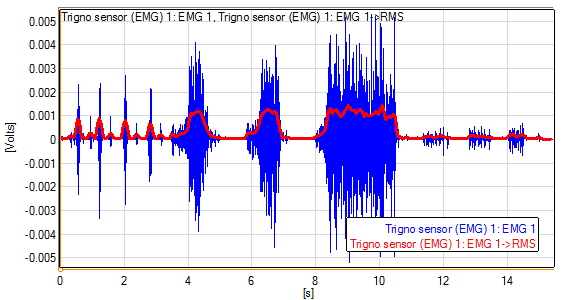
1. RMS value for a channel i: $$ RMS_i=\sqrt{\frac{\sum_{j=1}^{n}\left(x_{i+j}-x_{i}\right)^{2}}{n}}, $$

RMS results on a moving window are presented here:

2. Number of zero-crossings $$ ZC= \frac{1}{2}\sum\limits_{i=2}^{N} |sign(a_i) - sign(a_{i-1})| $$ where sign(x) returns 1 if x is positive and 0 otherwise.

   In a threshold using approach, you can calculate it on corssing the threshold

3. Activity detection

   The value of zero-crossings, after considering the dead zone, can be used to determin the begining of the contraction.

Normalization

The normalization operation is one of the basic requirements for effective classification. In the analysis of EMG signals, the amplitude of the EMG signal depends on individual characteristics, electrode location, and physical parameters of the electrode-skin contact. Typically, to obtain repeatable EMG signal effects, it is normalized relative to the maximum contraction of any muscle, meaning the EMG signal value during which the user generates maximum muscle contraction force (e.g. gripping a fist).

The normalization coefficient can be determined separately for each channel/muscle. The most commonly used value is the RMS value in a 500ms or longer window (depending on the duration of the contraction). The maximum observed RMS value for a given channel is usually taken as the coefficient value. $$ norm_i = max(RMS_i)
$$

Signal normalization: $$ ^{norm}x_i = x_1/norm_i $$

Tasks, part 2

1. Load the MVC signal and the training signal
2. Write rms and zc functions that for each channel (columns_emg) will estimate the features described above

    feature_rms = rms(signal, window=500, stride=100, fs=5120, columns_emg=['EMG_8', 'EMG_9'])# window length and stride given in [ms]
    
    feature_zc = zc(signal, threshold=0.1, window=500, stride=100, fs=5120, columns_emg=['EMG_8', 'EMG_9'])# window length and stride given in [ms]

3. Analyzing column TRAJ_GT you should notice geasture 0, corresponding to lack of movement (arm is in the neutral state) (more on the gestures can be found here). For each channel, determine the threshold value for the zc function, assuming that the threshold is the value that covers 95% of all noise samples. You can use numpy.percentile.

   threshold = find_threshold(signal, columns_emg=['EMG_8', 'EMG_9'], column_gesture='TRAJ_GT', idle_gesture_id = 0)
   

4. Write function norm_emg that normalizes the EMG signal

    norm_coeffs = rms(signal_mvc, window=500, stride=100, fs=5120, columns_emg=['EMG_8', 'EMG_9']).max()
    norm_emg = norm_emg(signal, norm_coeffs, columns_emg=['EMG_8', 'EMG_9'])

_{Developed based on instructions for HMI laboratories by Piotr Kaczmarek}

_{Author: Kamil Młodzikowski}